Proof of Isoquants Properties

Links to all courses
1. Isoquants have a negative slope that is the curve is downward to the right.
Proof:

Figure 1 shows the amount of x1 increases but x2 remains constant. It cannot be so in isoquant. 
Figure 2 shows amount of x2 increases but x1 is constant. It also is not the case.
Figure 3 shows that both x1 & x2 increase. This too can't happen.
Therefore, only possibility is that, IQC is downward to the right. 
[Proved]
2. Isoquants are convex to the origin.
Proof:

 Figure 5 shows concavity of the IQC to the origin. It implies that Marginal rate of technical substitution (MRTS) increases as more and more of x1 is substituted for x2. This violates the assumption of IQC.
Figure 6 shows IQC to be convex to the origin. Only a convex IQC implies a diminishing MRTS of x1 for x2. 

3. Isoquants cannot intersect or be tangent to each other
Proof:

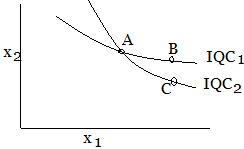
Let two IQC's intersect each other at point A. 
So, for IQC1, A = B (as quantity is same at any point in IQC)
For IQC2, A = C
So, B = C
But as two isoquants represent different quantity, B & C can never be equal. 
So, isoquants cannot intersect or be tangent to each other. [Proved]

4. Higher IQC's represents a higher level of output than the lower ones.
Proof:

Consider a vertical movement from point a of IQC1 to point b of IQC2. It implies increase in input x2. 
Consider a horizontal movement from point of IQC1 to point d of IQC2. It implies increase in input x1. 
Consider a diagonal movement from point a to point c. It implies increase in both x1 & x2. 
As increase in input yields increase in quantity, upper or higher IQC represents a higher level of output.